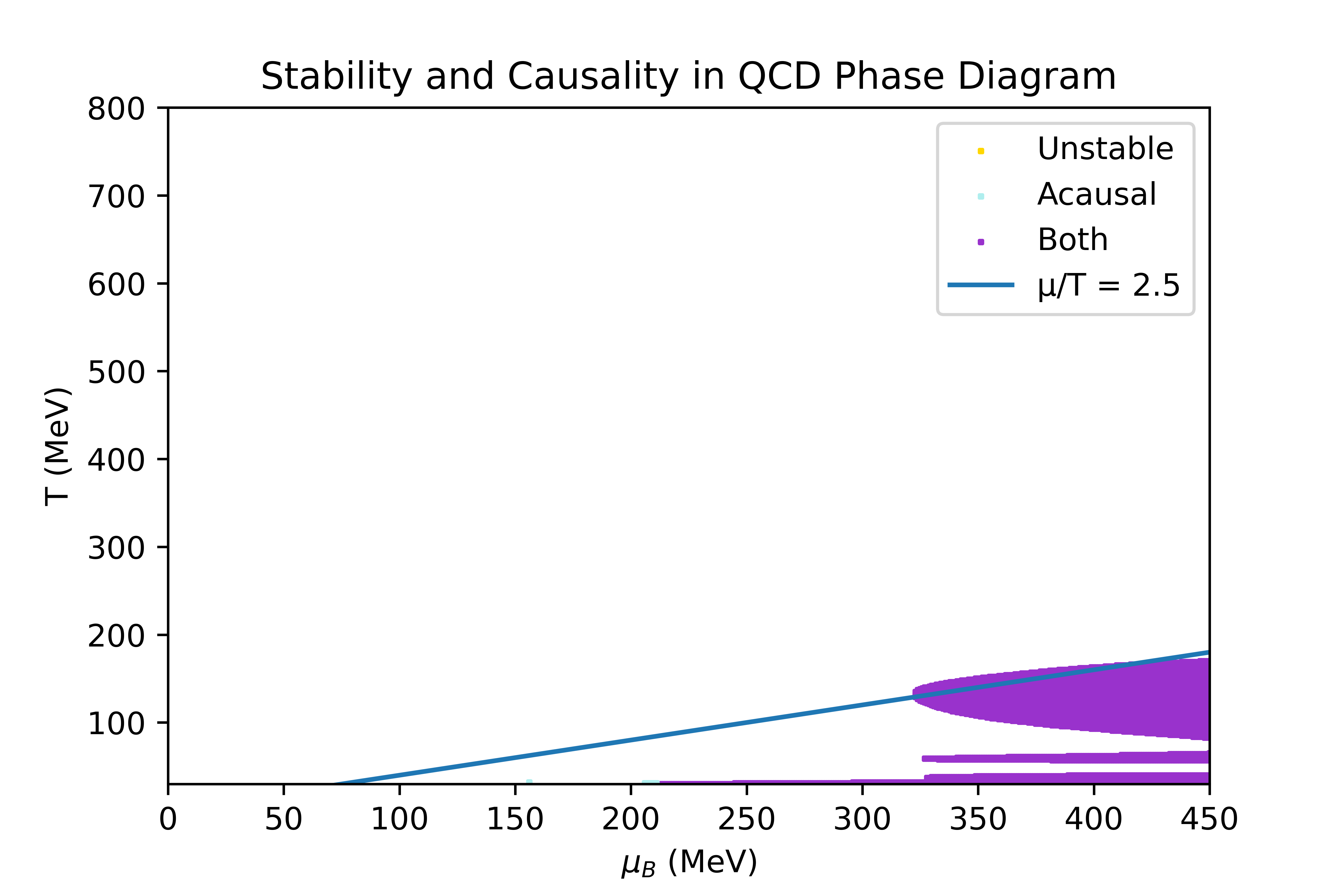
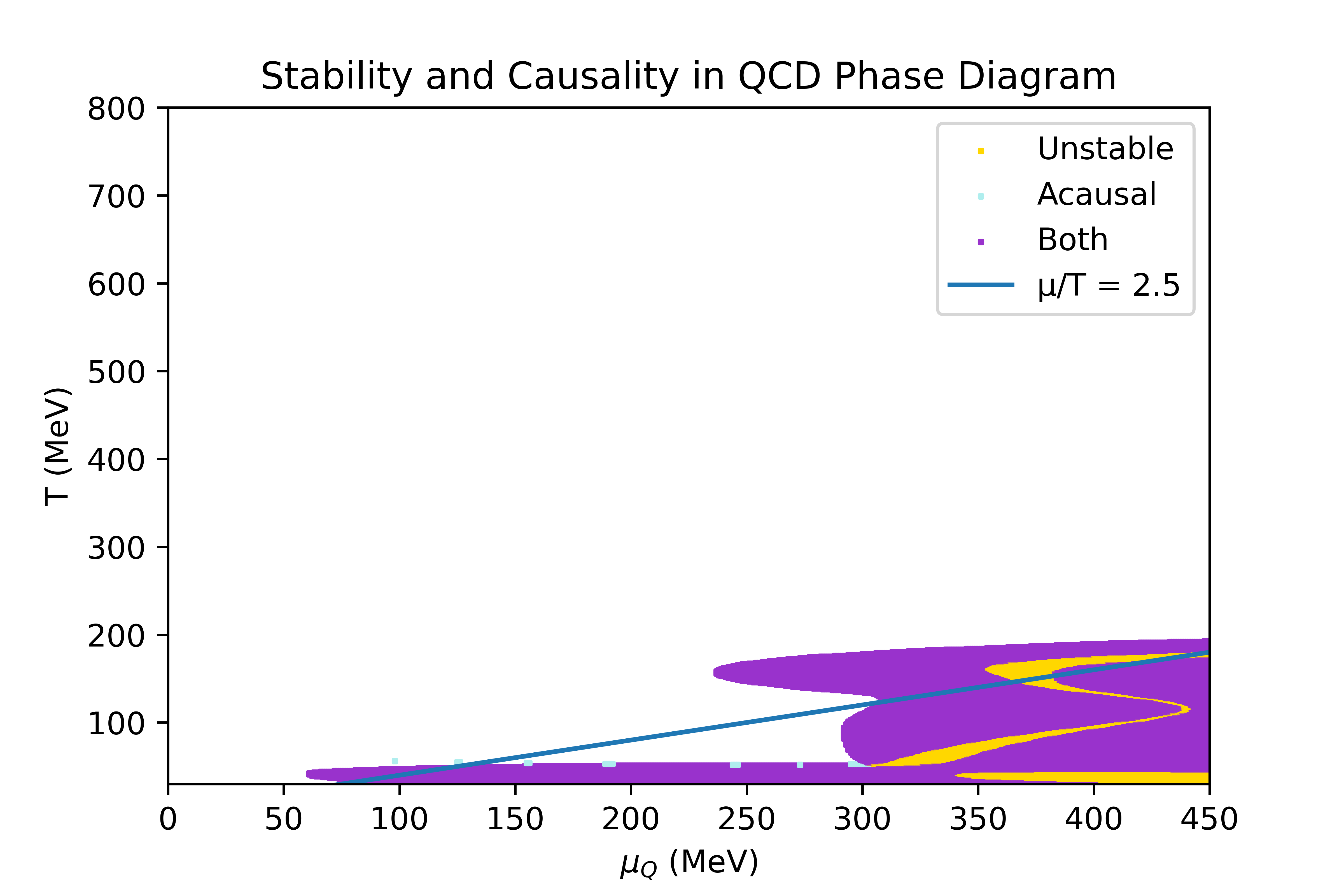
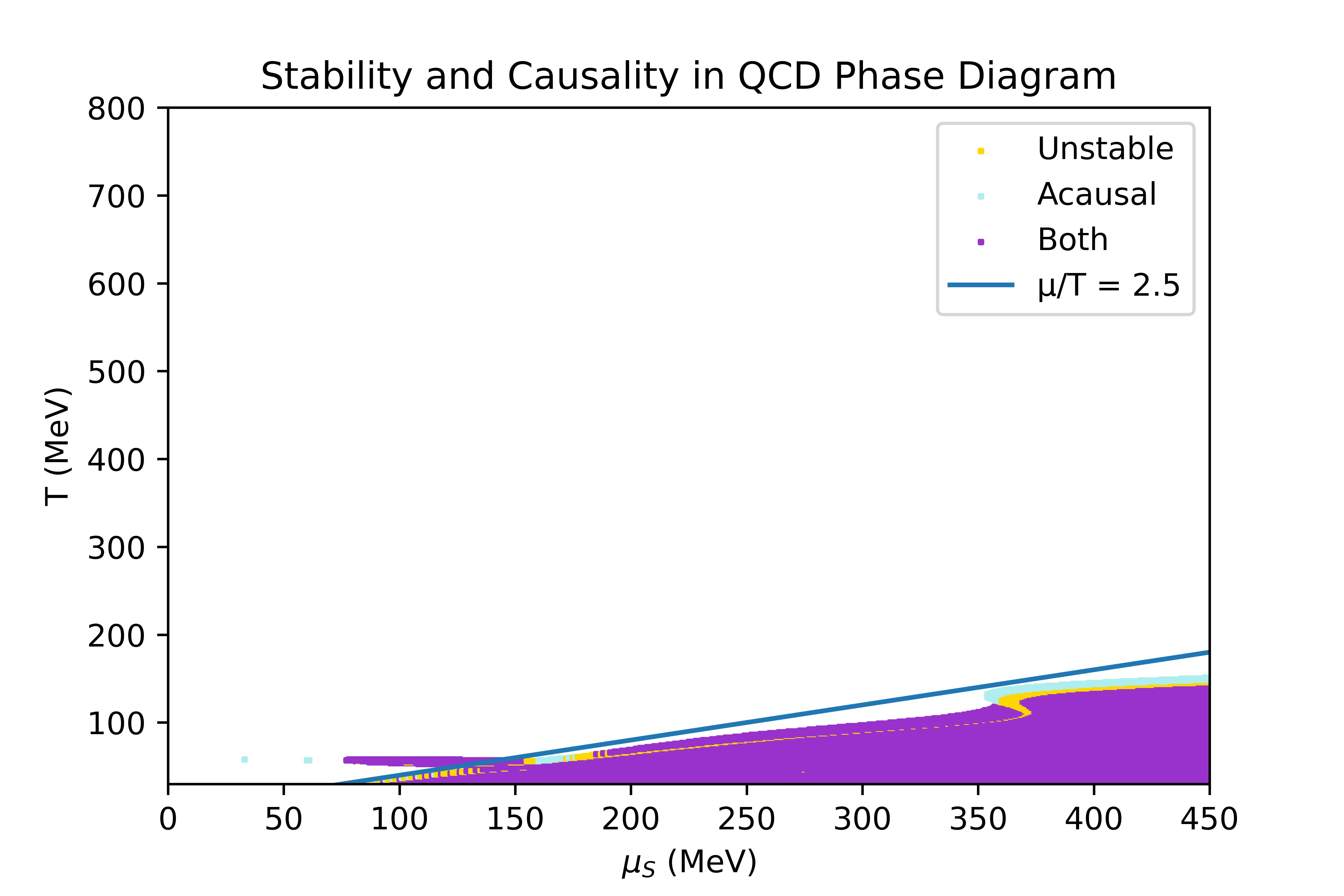
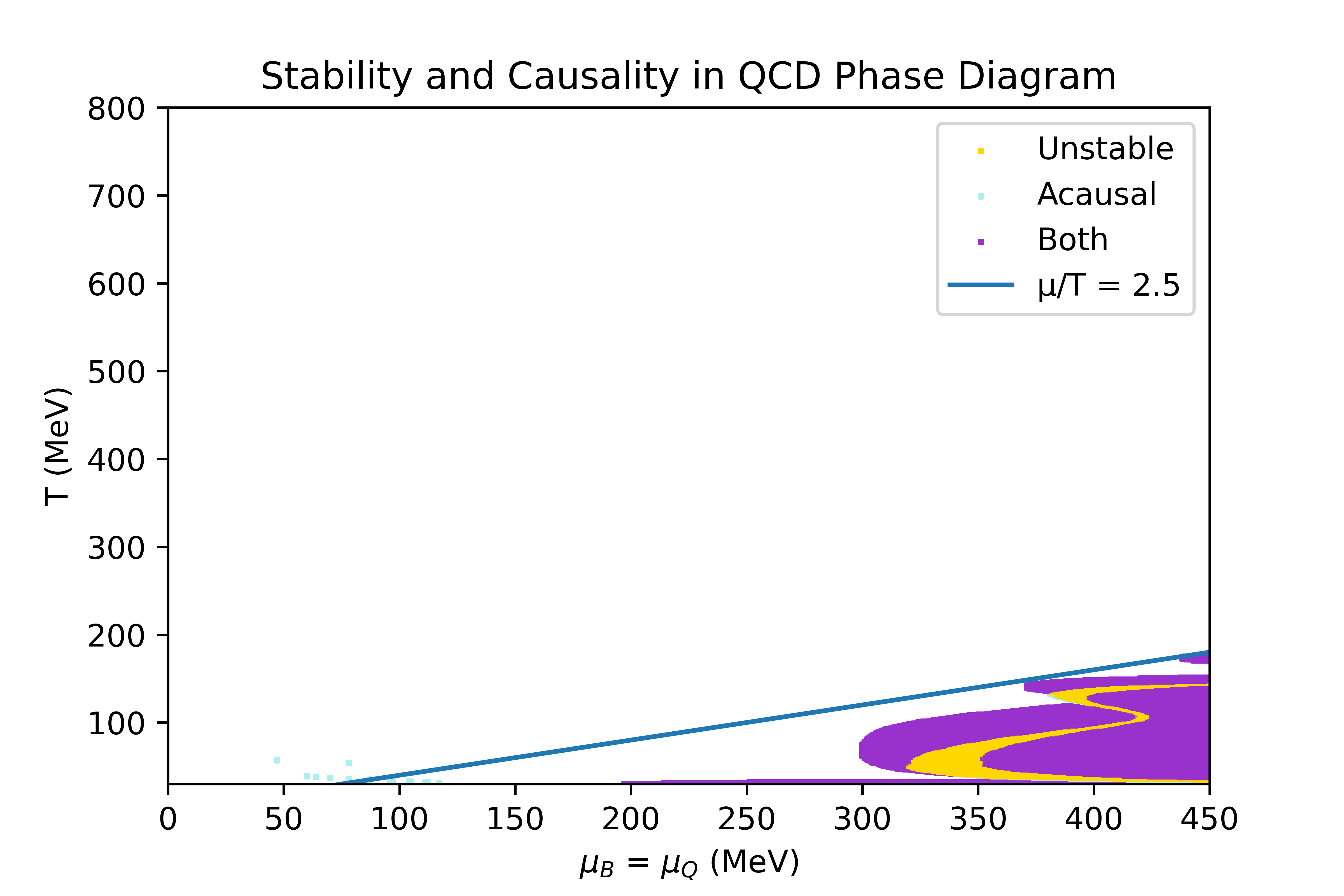
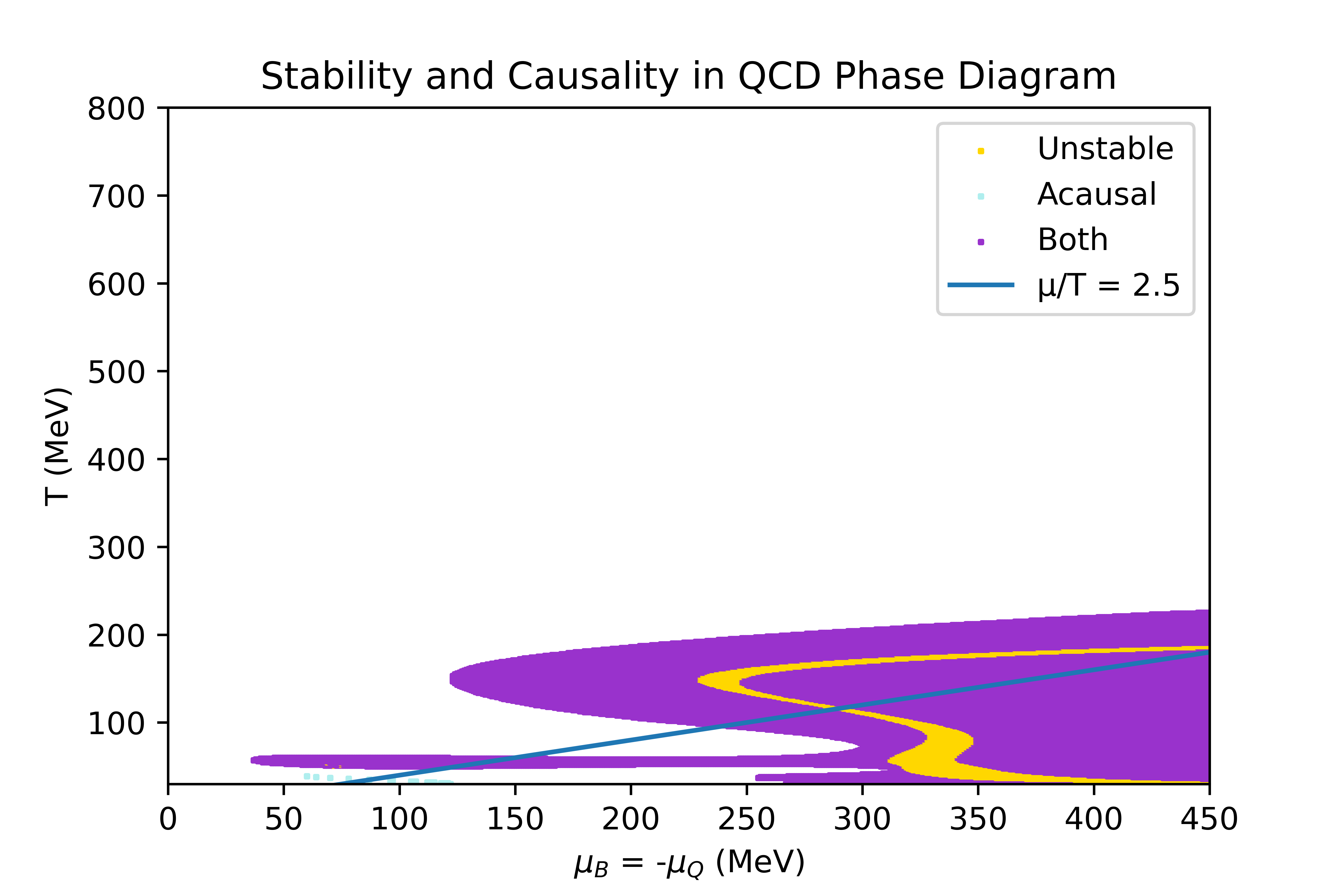
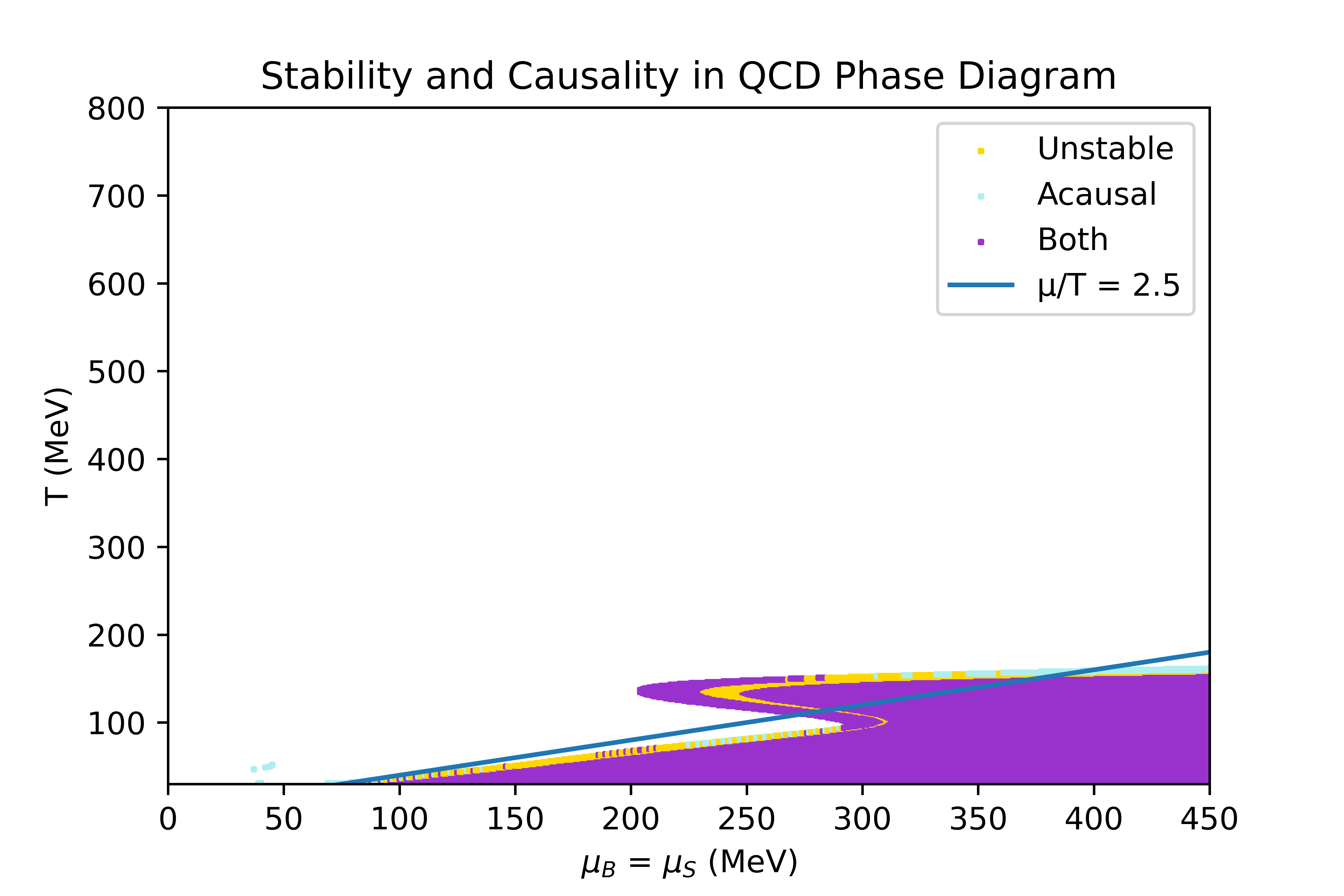
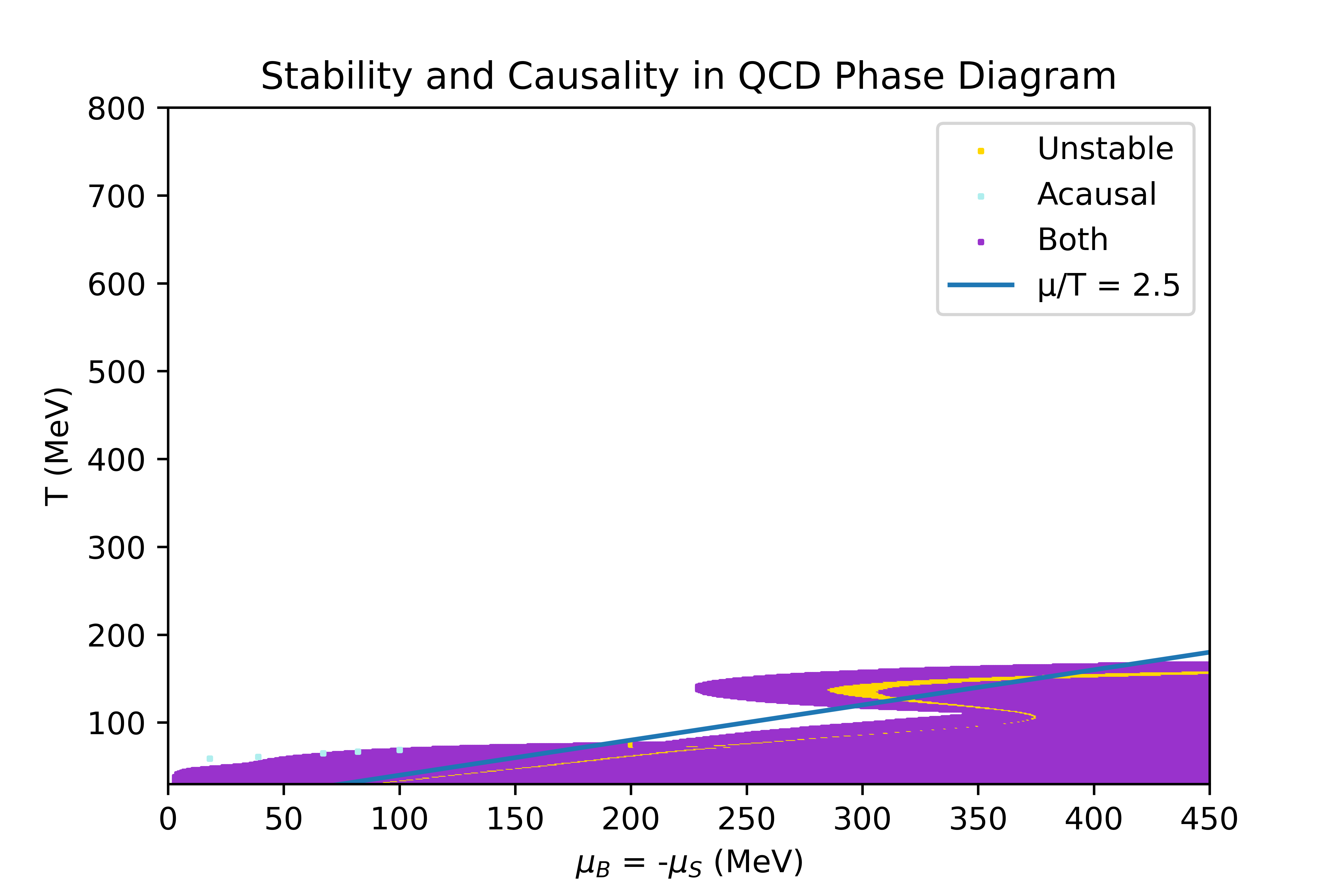
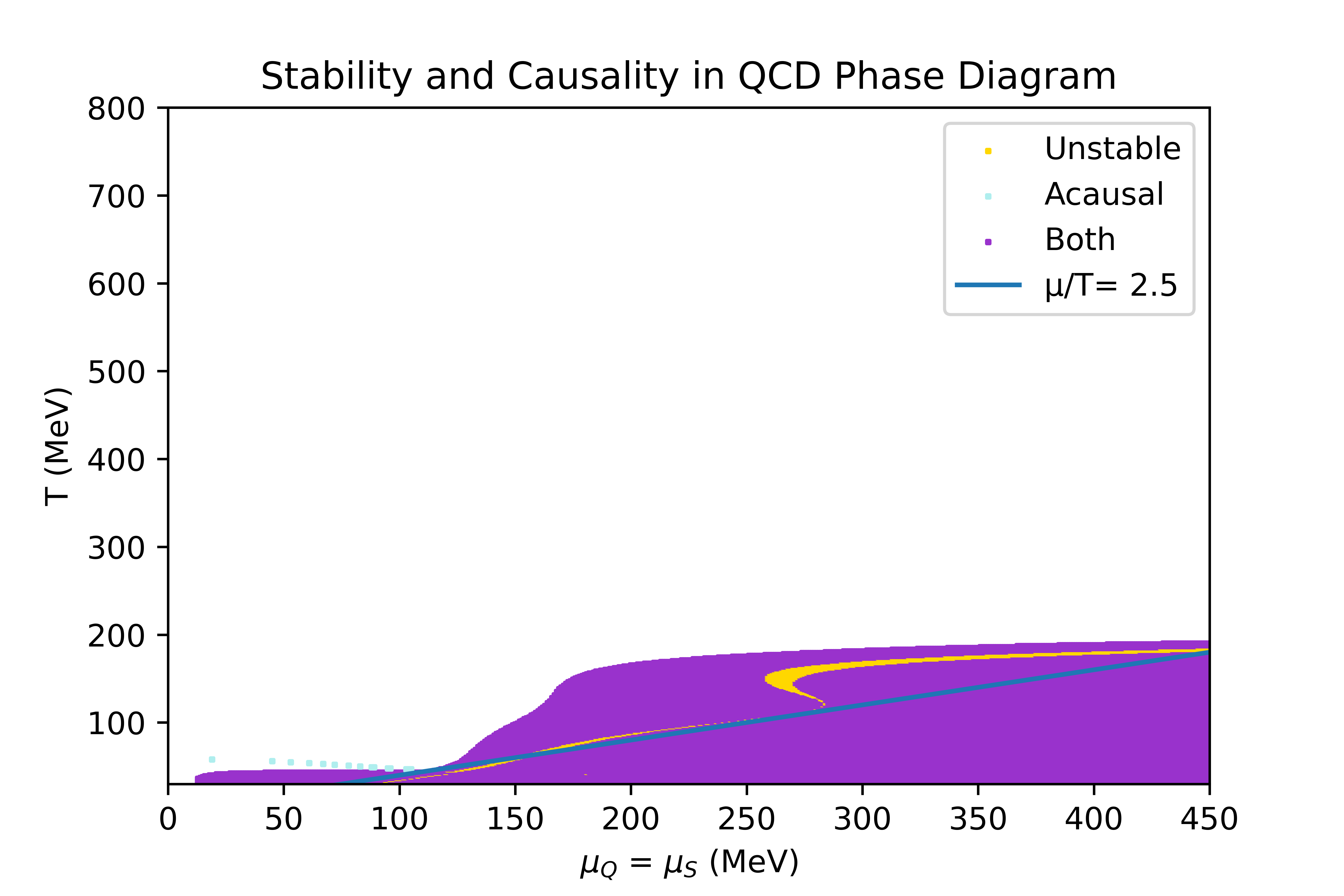
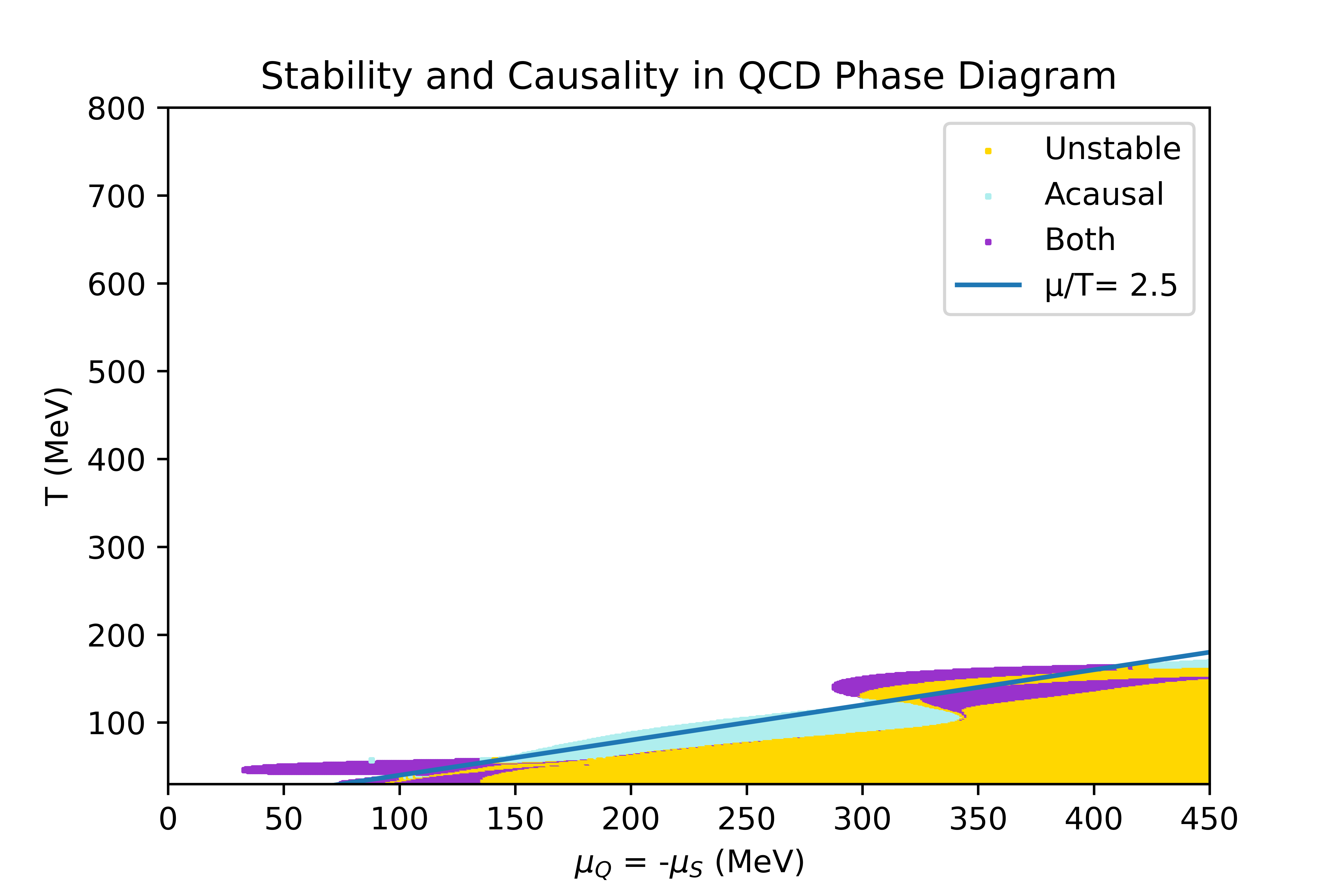
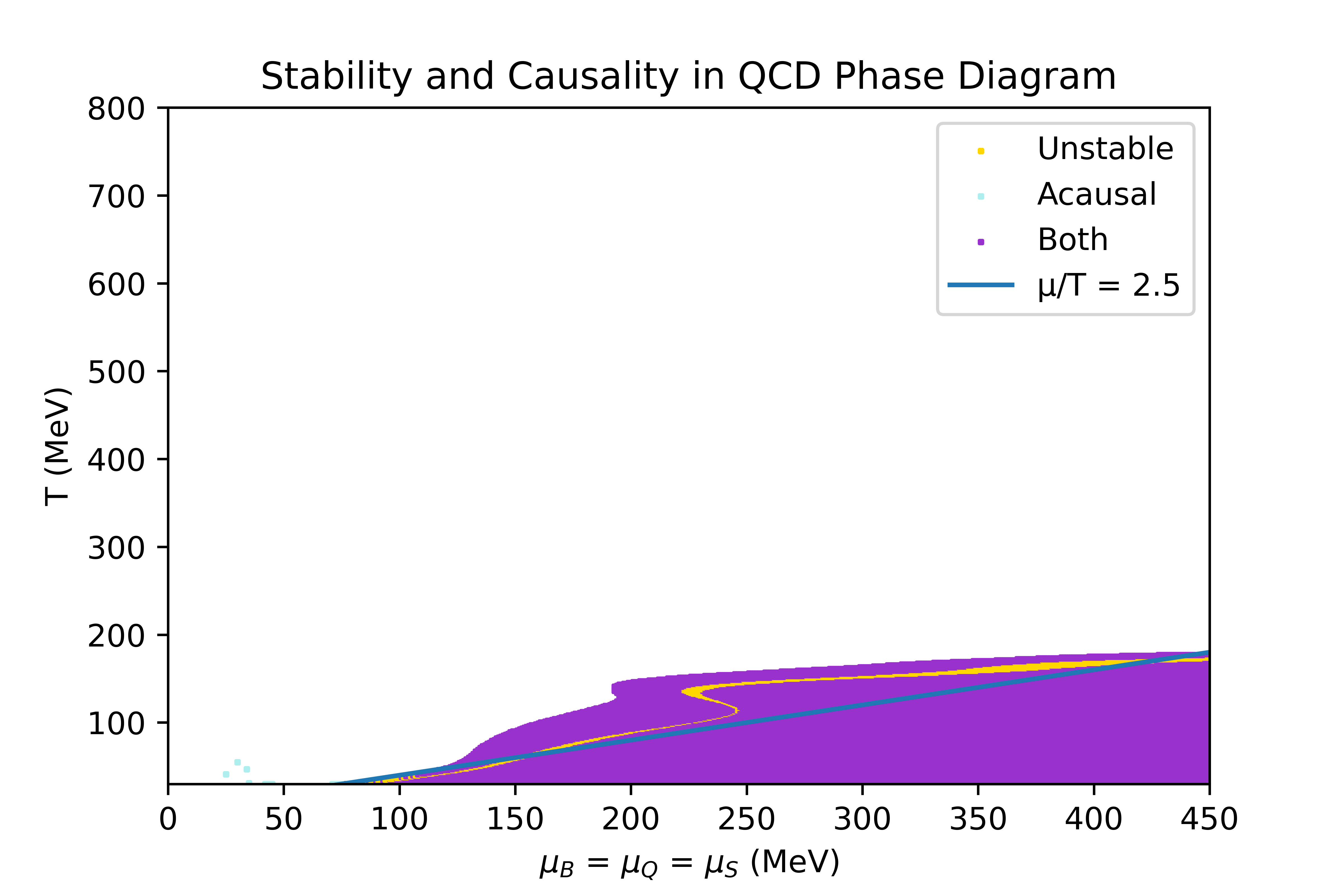
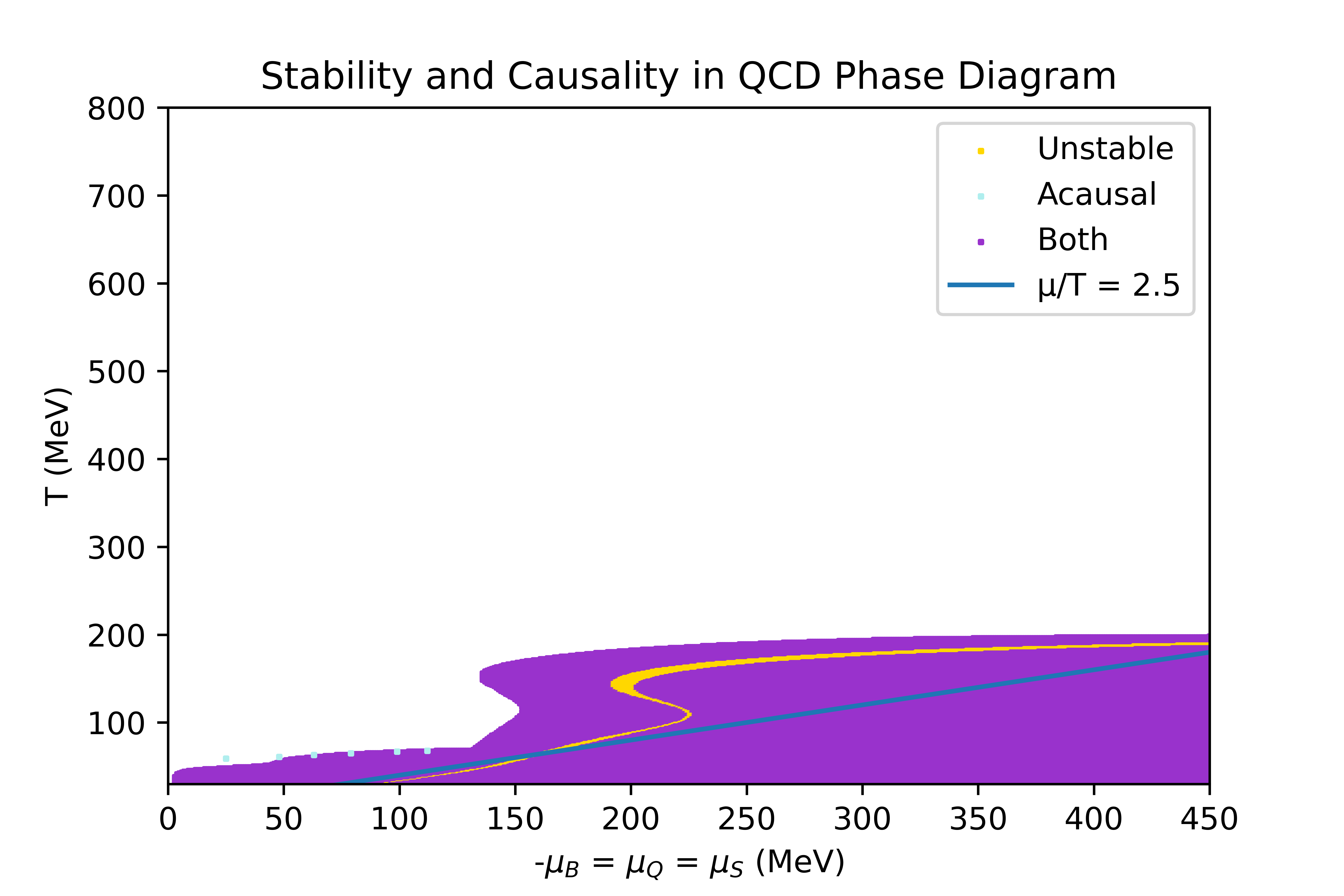
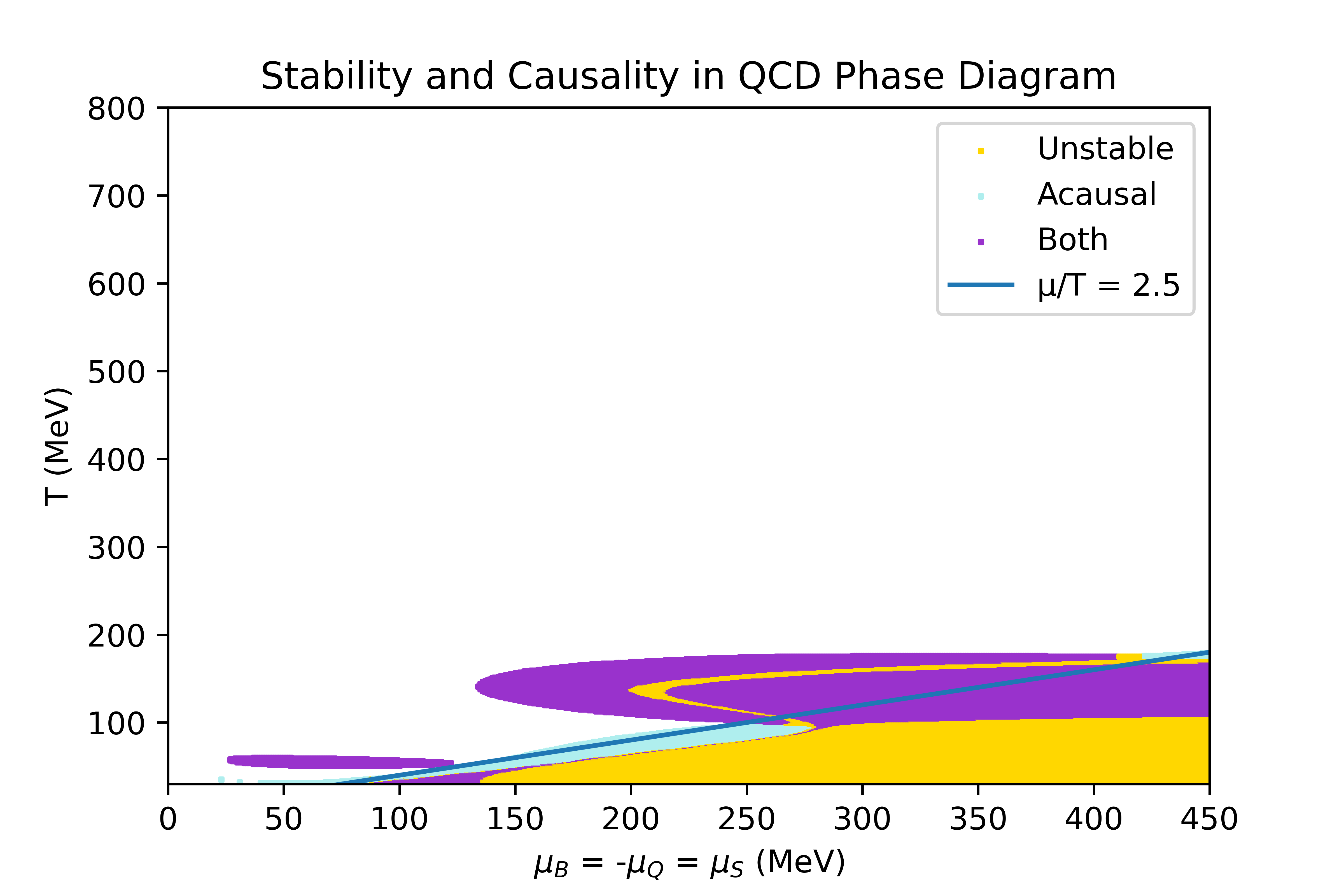
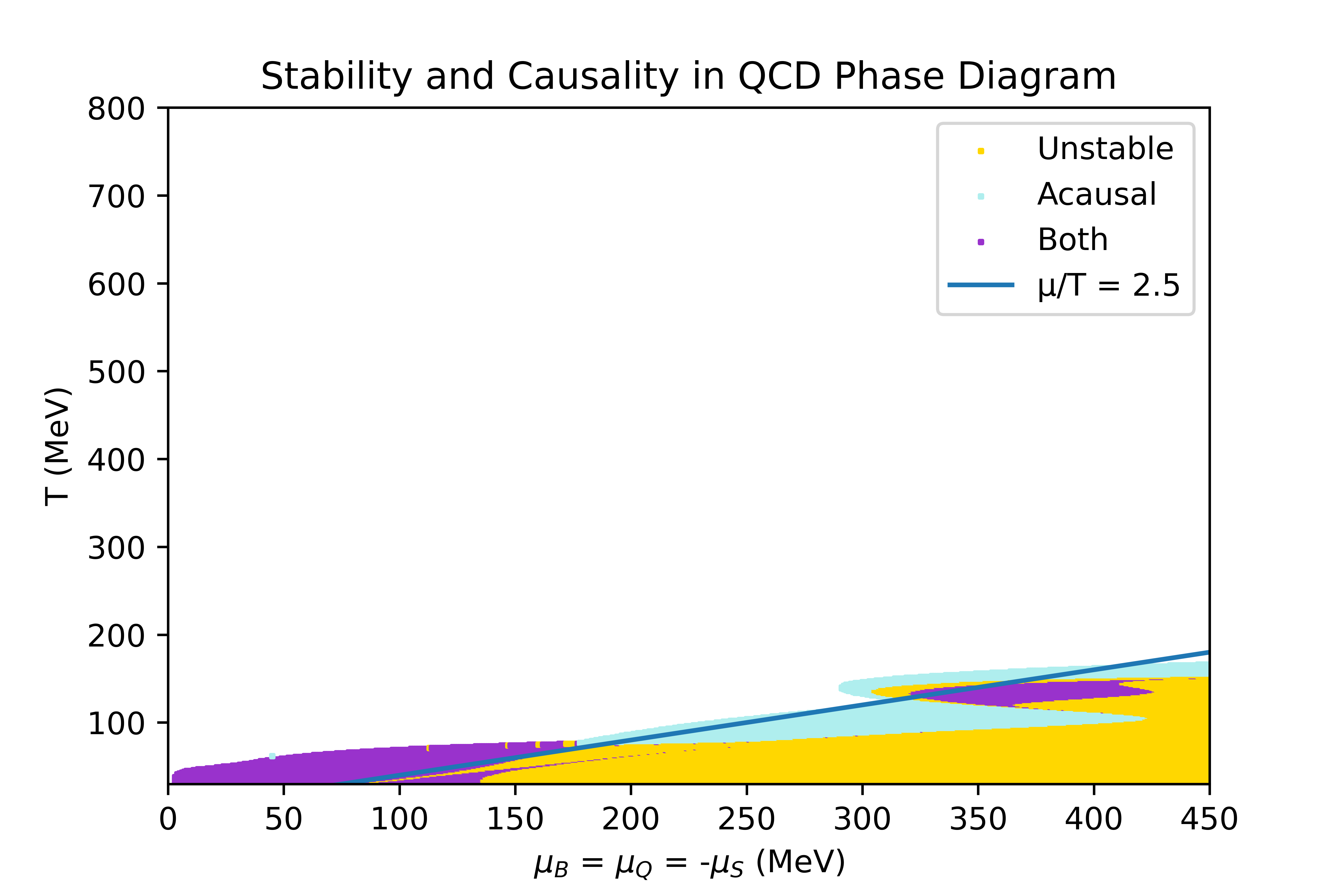
The limits of the regions where the equation of state obtained through the 4D Taylor expansion, described in the Physics overview, is stable and causal have been studied. In this section, the conditions studied to determine the stability criteria are explicited, and the result obtained in some particular directions of finite chemicals potentials are shown.
Stability conditions
To verify to stability of an equation of state depending on \(T\), \(\mu_B\), \(\mu_Q\) and \(\mu_S\), one needs to make sure that the \(4 \times 4\) Hessian matrix \(M\) of pressure \(P(T, \mu_B, \mu_Q, \mu_S)\) is positive definite :
\[\begin{split}M=\begin{bmatrix}
\frac{\partial s}{\partial T}\big|_{\vec{\mu}} & \frac{\partial s}{\partial \mu_B}\big|_{T,\mu_S,\mu_Q} & \frac{\partial s}{\partial \mu_S}\big|_{T,\mu_B,\mu_Q} & \frac{\partial s}{\partial \mu_Q}\big|_{T,\mu_B,\mu_S} \\
\frac{\partial n_B}{\partial T}\big|_{\vec{\mu}} & \chi_2^B & \chi_{11}^{BS} & \chi_{11}^{BQ} \\
\frac{\partial n_S}{\partial T}\big|_{\vec{\mu}} & \chi_{11}^{SB} & \chi_2^S & \chi_{11}^{SQ} \\
\frac{\partial n_Q}{\partial T}\big|_{\vec{\mu}} & \chi_{11}^{QB} & \chi_{11}^{QS} & \chi_2^Q
\end{bmatrix} \; .\end{split}\]
This means that each submatrix should have a positive or null determinant.
For the \(3 \times 3\) submatrix of conserved charges chemical potentials, it is equivalent to verify that:
\[\begin{split}\chi^B_2 \geq 0 \; , \\
\chi^Q_2 \geq 0 \; , \\
\chi^S_2 \geq 0 \; ,\end{split}\]
\[\begin{split}\chi^B_2 \chi^Q_2 \geq (\chi^{BQ}_{11})^2 \; , \\
\chi^B_2 \chi^S_2 \geq (\chi^{BS}_{11})^2 \; , \\
\chi^Q_2 \chi^S_2 \geq (\chi^{QS}_{11})^2 \; ,\end{split}\]
and
\[\chi^B_2 \chi^Q_2 \chi^S_2 + 2 \left(\chi^{BQ}_{11} \chi^{BS}_{11} \chi^{QS}_{11}\right) \geq \chi^{B}_{2} \left(\chi^{QS}_{11}\right)^2 + \chi^{Q}_{2} \left(\chi^{BS}_{11}\right)^2 + \chi^{S}_{2} \left(\chi^{BQ}_{11}\right)^2 \; .\]
To verify the positivity of the entire \(4 \times 4\) Hessian matrix, one has to take into account the additional terms involving \(T\), leading to the following additional conditions to verify:
\[\frac{\partial s}{\partial T}\bigg|_{\vec{\mu}} \geq 0 \; ,\]
\[\begin{split}\chi_2^B \frac{\partial s}{\partial T}\bigg|_{\vec{\mu}} \geq \left[\frac{\partial s}{\partial \mu_B}\bigg|_{T,\mu_S,\mu_Q}\right]^2 \; , \\
\chi_2^S \frac{\partial s}{\partial T}\bigg|_{\vec{\mu}} \geq \left[\frac{\partial s}{\partial \mu_S}\bigg|_{T,\mu_B,\mu_Q}\right]^2 \; , \\
\chi_2^Q \frac{\partial s}{\partial T}\bigg|_{\vec{\mu}} \geq \left[\frac{\partial s}{\partial \mu_Q}\big|_{T,\mu_B,\mu_S}\right]^2 \; ,\end{split}\]
\[\begin{split}\frac{\partial s}{\partial T}\bigg|_{\vec{\mu}}\left[\chi_2^B\chi_2^S-\left(\chi_{11}^{BS}\right)^2\right] + 2\chi_{11}^{BS}\frac{\partial s}{\partial \mu_B}\bigg|_{T,\mu_S,\mu_Q} \frac{\partial s}{\partial \mu_S}\bigg|_{T,\mu_B,\mu_Q} \geq \hspace{2cm} \\
\hspace{2cm} \chi_2^B \left(\frac{\partial s}{\partial \mu_S}\bigg|_{T,\mu_B,\mu_Q}\right)^2+\chi_2^S \left(\frac{\partial s}{\partial \mu_B}\bigg|_{T,\mu_S,\mu_Q}\right)^2 \; , \\\end{split}\]
\[\begin{split}\frac{\partial s}{\partial T}\bigg|_{\vec{\mu}}\left[\chi_2^B\chi_2^Q-\left(\chi_{11}^{BQ}\right)^2\right] +2\chi_{11}^{BQ}\frac{\partial s}{\partial \mu_B}\bigg|_{T,\mu_S,\mu_Q} \frac{\partial s}{\partial \mu_Q}\bigg|_{T,\mu_B,\mu_S} \geq \hspace{2cm} \\
\hspace{2cm} \chi_2^B \left(\frac{\partial s}{\partial \mu_Q}\bigg|_{T,\mu_B,\mu_S}\right)^2+\chi_2^Q \left(\frac{\partial s}{\partial \mu_B}\bigg|_{T,\mu_S,\mu_Q}\right)^2 \; , \\\end{split}\]
\[\begin{split}\frac{\partial s}{\partial T}\bigg|_{\vec{\mu}}\left[\chi_2^S\chi_2^Q-\left(\chi_{11}^{SQ}\right)^2\right] +2\chi_{11}^{SQ}\frac{\partial s}{\partial \mu_S}\bigg|_{T,\mu_B,\mu_Q} \frac{\partial s}{\partial \mu_Q}\bigg|_{T,\mu_B,\mu_S} \geq \hspace{2cm} \\
\hspace{2cm} \chi_2^S \left(\frac{\partial s}{\partial \mu_Q}\bigg|_{T,\mu_B,\mu_S}\right)^2 +\chi_2^Q \left(\frac{\partial s}{\partial \mu_S}\bigg|_{T,\mu_B,\mu_Q}\right)^2 \; ,\end{split}\]
and
\[\begin{split}\frac{\partial s}{\partial T}\bigg|_{\vec{\mu}}\left[\chi_2^B\chi_2^S\chi_2^Q+2\chi_{11}^{BS}\chi_{11}^{SQ}\chi_{11}^{BQ}-\sum_{j=B,S,Q}\chi_2^j \left(\chi_{11}^{j+1,j+2}\right)^2\right] \hspace{5cm} \\
+ \sum_{j=B,S,Q}\left[\left(\chi_{11}^{j,j+1}\right)^2-\chi_2^j\chi_2^{j+1}\right]\left(\frac{\partial s}{\partial \mu_{j+2}}\bigg|_{T,\mu_{\neq j+2}}\right)^2 \hspace{5cm} \\
\hspace{1cm}+ 2 \sum_{j=B,S,Q}\left[ \chi_2^j\chi_{11}^{j+1,j+2}-\chi_{11}^{j,j+1}\chi_{11}^{j,j+2} \right]\frac{\partial s}{\partial \mu_{j+1}}\bigg|_{T,\mu_{\neq j+1}}\frac{\partial s}{\partial \mu_{j+2}}\bigg|_{T,\mu_{\neq j+2}} < 0 \; .\end{split}\]